全加器/(1 bit)Full Adder
1. 全加器定义
全加器(FA)是能够计算低位进位的二进制逻辑电路元件
2. 全加器真值表及逻辑表达式
| Ai |
Bi |
Ci−1(Carry) |
Si(Sum) |
Ci |
| 0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
| 0 |
1 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
0 |
| 1 |
0 |
1 |
0 |
1 |
| 1 |
1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
1 |
逻辑表达式:
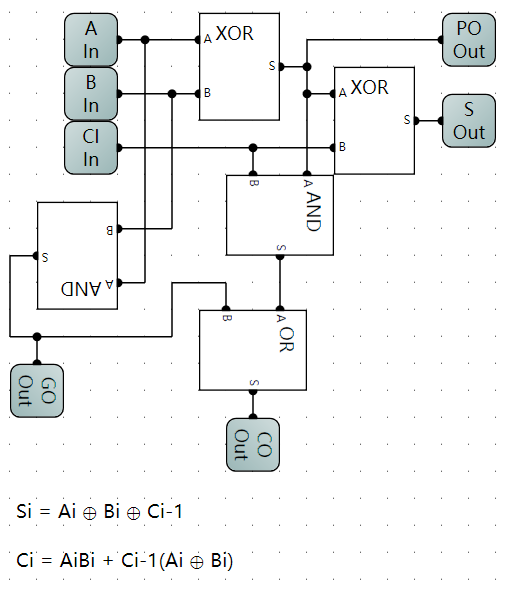
Si=Ai⨁Bi⨁Ci−1
Ci=Ai⋅Bi+Ci−1⋅(Ai+Bi)
或
Ci=Ai⋅Bi+Ci−1⋅(Ai⨁Bi)
补充:真值表的最小逻辑表达式
已知逻辑函数F关于多个逻辑变量的真值表,首先找到所有F=1的行,在这些行中,将值为0的若干个逻辑变量取反(使其变为1),而值为1的变量保持不变,将该行所有变量逻辑与(将所有变量逻辑值相关联)得到该行子逻辑式,然后将这些行逻辑子式逻辑或,最后化简得到最小逻辑表达式
例如,观察输入Ai、Bi、Ci−1(逻辑变量Xni)与输出Si,找到Si=1的行
| Ai |
Bi |
Ci−1 |
Si |
| 0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
1 |
| 1 |
0 |
0 |
1 |
| 1 |
1 |
1 |
1 |
即Si=(Ai⋅Bi⋅Ci−1)+(Ai⋅Bi⋅Ci−1)+(Ai⋅Bi⋅Ci−1)+(Ai⋅Bi⋅Ci−1)
合并化简,提取Ci−1,Ci−1,
即Si=Ci−1⋅(Ai⋅Bi+Ai⋅Bi)+Ci−1⋅(Ai⋅Bi+Ai⋅Bi)
由异或(逻辑代数运算基本公式)换算可得
Si=Ai⨁Bi⨁Ci−1(此步换算对于“基础与或非”而言并非化简,但如果XOR被封装,不考虑XOR的实现则此式更便于理解)
3. 全加器逻辑电路示意图