逻辑门电路/LGC

基础逻辑电路:与门、或门、非门

  1. 与门/AND

    1. 与门真值表
      A B S
      0 0 0
      0 1 0
      1 0 0
      1 1 1
    2. 与门逻辑电路示意图

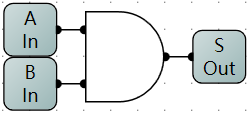
  2. 或门/OR

    1. 或门真值表
      A B S
      0 0 0
      0 1 1
      1 0 1
      1 1 1
    2. 或门逻辑电路示意图

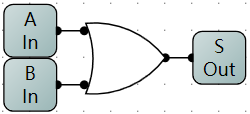
  3. 非门/NOT

    1. 非门真值表
      A S
      1 0
      0 1
    2. 非门逻辑电路示意图

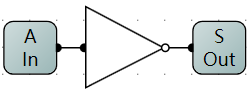
其他常见(逻辑)门电路

  1. 与非门

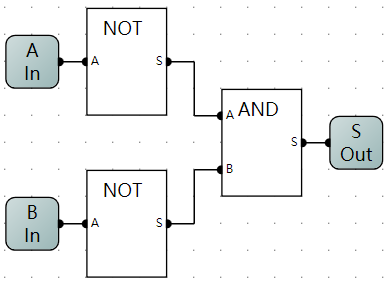
    1. 与非门真值表
      A B S
      0 0 1
      0 1 1
      1 0 1
      1 1 0
    2. 与非门逻辑表达式

      S=A⋅B‾=A‾+B‾\begin{aligned} S = \overline{A\cdot B} = \overline{A} + \overline{B} \end{aligned}

    3. 与非门逻辑电路示意图


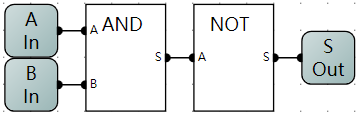
      OR\begin{aligned} OR \end{aligned}

  2. 或非门

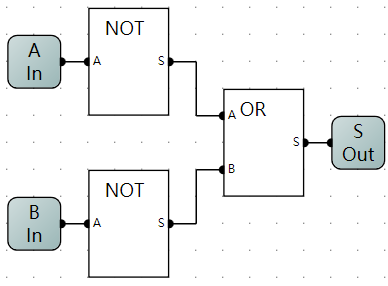
    1. 或非门真值表
      A B S
      0 0 1
      0 1 0
      1 0 0
      1 1 0
    2. 或非门逻辑表达式

      S=A+B‾=A‾⋅B‾\begin{aligned} S = \overline{A + B} = \overline{A} \cdot \overline{B} \end{aligned}

    3. 或非门逻辑电路示意图


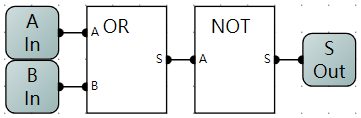
      OR\begin{aligned} OR \end{aligned}

  3. 异或门

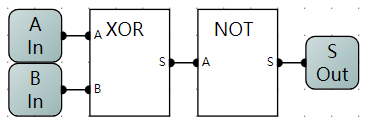
    1. 异或门真值表
      A B S
      0 0 0
      0 1 1
      1 0 1
      1 1 0
    2. 异或门逻辑表达式

      S=A‾⋅B+A⋅B‾=(A+B)⋅(A‾+B‾)=A⨀B‾=A⨁B\begin{aligned} S = \overline{A} \cdot B + A \cdot \overline{B} = (A + B) \cdot (\overline{A} + \overline{B}) = \overline{A \bigodot B} = A \bigoplus B \end{aligned}

    3. 异或门逻辑电路示意图


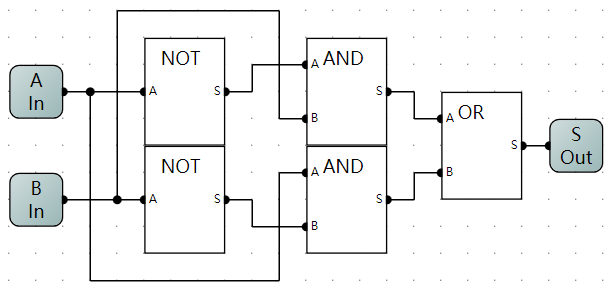
      OR\begin{aligned} OR \end{aligned}

  4. 同或门

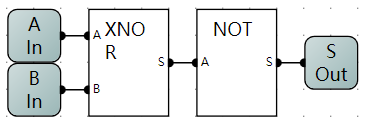
    1. 同或门真值表
      A B S
      0 0 1
      0 1 0
      1 0 0
      1 1 1
    2. 同或门逻辑表达式

      S=A‾⋅B‾+A⋅B=(A‾+B)⋅(A+B‾)=A⨁B‾=A⨀B\begin{aligned} S = \overline{A} \cdot \overline{B} + A \cdot B = (\overline{A} + B) \cdot (A + \overline{B}) = \overline{A \bigoplus B} = A \bigodot B \end{aligned}

    3. 同或门逻辑电路示意图


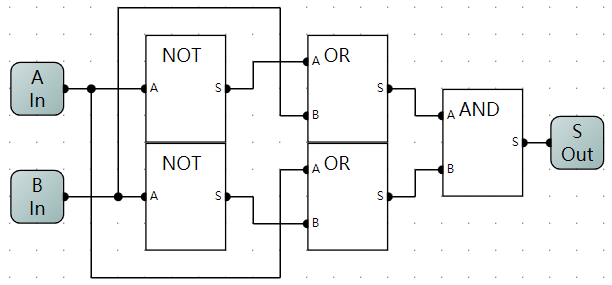
      OR\begin{aligned} OR \end{aligned}

补充：逻辑代数运算的基本公式

  1. 德·摩根定律(反演律)

A⋅B‾=A‾+B‾(式1.1)A+B‾=A‾⋅B‾(式1.2) \begin{aligned} \overline{A \cdot B} = \overline{A} + \overline{B} \qquad(式1.1) \\ \overline{A + B} = \overline{A} \cdot \overline{B} \qquad(式1.2) \end{aligned}

  1. 交换律、结合律与分配律

A+B=B+A(式2.1)A⋅B=B⋅A(式2.2)(A+B)+C=A+(B+C)(式2.3)(A⋅B)⋅C=A⋅(B⋅C)(式2.4)A⋅(B+C)=A⋅B+A⋅C(式2.5) \begin{aligned} A + B = B + A \qquad(式2.1) \\ A \cdot B = B \cdot A \qquad(式2.2) \\ (A + B) + C = A + (B + C) \qquad(式2.3) \\ (A \cdot B) \cdot C = A \cdot (B \cdot C) \qquad(式2.4) \\ A \cdot (B + C) = A \cdot B + A \cdot C \qquad(式2.5) \end{aligned}

  1. 与或非逻辑推断

0⋅A=0(式3.1)1⋅A=1(式3.2)A⋅A=A(式3.3)A⋅A‾=0(式3.4)0+A=A(式3.5)1+A=1(式3.6)A+A=A(式3.7)A+A‾=1(式3.8) \begin{aligned} 0 \cdot A = 0 \qquad(式3.1) \\ 1 \cdot A = 1 \qquad(式3.2) \\ A \cdot A = A \qquad(式3.3) \\ A \cdot \overline{A} = 0 \qquad(式3.4) \\\\ 0 + A = A \qquad(式3.5) \\ 1 + A = 1 \qquad(式3.6) \\ A + A = A \qquad(式3.7) \\ A + \overline{A} = 1 \qquad(式3.8) \end{aligned}

  1. 其他

A⋅(A+B)=A(式4.1) \begin{gathered} A \cdot (A + B) = A \qquad(式4.1) \\ \end{gathered}

证明:原式扩写为A⋅A‾+A⋅(A+B),提取A,则A⋅(A‾+A+B)=A⋅(1+B)=A⋅1=A,得证 \begin{gathered} 证明:原式扩写为A \cdot \overline{A} + A \cdot (A + B),提取A,则A \cdot (\overline{A} + A + B) = A \cdot (1 + B) = A \cdot 1 = A,得证 \\ \end{gathered}

注解:在由若干个不定项组成的逻辑与运算的所有项中，只存在一个单逻辑值项时，此单逻辑值具有的强决定性 \begin{gathered} 注解:在由若干个不定项组成的逻辑与运算的所有项中，只存在一个单逻辑值项时，此单逻辑值具有的强决定性 \\\\\\ \end{gathered}

A+A⋅B=A(式4.2) \begin{gathered} A + A \cdot B = A \qquad(式4.2) \\ \end{gathered}

证明:原式扩写为A⋅A+A⋅B,提取A,得A⋅(A+B),由式4.1可知,结果为A,得证 \begin{gathered} 证明:原式扩写为A \cdot A + A \cdot B,提取A,得A \cdot (A + B), 由式4.1可知,结果为A,得证 \\ \end{gathered}

注解:在由若干个不定项组成的逻辑或运算的所有项中，只存在一个单逻辑值项时，此单逻辑值具有的强决定性 \begin{gathered} 注解:在由若干个不定项组成的逻辑或运算的所有项中，只存在一个单逻辑值项时，此单逻辑值具有的强决定性 \\\\\\ \end{gathered}

A⋅B⋅(A+B)=A⋅B(式4.3) \begin{gathered} A \cdot B \cdot (A + B) = A \cdot B \qquad(式4.3) \\ \end{gathered}

证明:由分配律得A⋅A⋅B+A⋅B⋅B=A⋅B+A⋅B=A⋅B,得证 \begin{gathered} 证明:由分配律得A \cdot A \cdot B + A \cdot B \cdot B = A \cdot B + A \cdot B = A \cdot B,得证 \\\\\\ \end{gathered}

A⋅B+(A+B)=(A+B)(式4.4) \begin{gathered} A \cdot B + (A + B) = (A + B) \qquad(式4.4) \\ \end{gathered}

证明:原式扩写为A⋅B+A⋅A+B,提取A,得A⋅(A+B)+B=(A+B),得证 \begin{gathered} 证明:原式扩写为A \cdot B + A \cdot A + B,提取A,得A \cdot (A + B) + B = (A + B),得证 \\\\\\ \end{gathered}

A+B⋅C=(A+B)⋅(A+C)→当C=A‾A+A‾⋅B=A+B(式4.5) \begin{gathered} A + B \cdot C = (A + B) \cdot (A + C) \xrightarrow{当C = \overline{A}} A + \overline{A} \cdot B = A + B \qquad(式4.5) \\ \end{gathered}

证明:原式扩写为A⋅(A+B+C)+B⋅C(说明:将(B+C)看成一个整体X,以此类推,还可以将(B+C+D+⋯ )看成整体),故原式化为A⋅A+A⋅B+A⋅C+B⋅C=(A+B)⋅(A+C),得证 \begin{gathered} 证明:原式扩写为A \cdot (A + B + C) + B \cdot C(说明:将(B + C)看成一个整体X,以此类推,还可以将(B + C + D + \cdots)看成整体),故原式化为A \cdot A + A \cdot B + A \cdot C + B \cdot C = (A + B) \cdot (A + C),得证 \\\\\\ \end{gathered}

A⋅B+A‾⋅C+B⋅C=A⋅B+A‾⋅C(式4.6) \begin{gathered} A \cdot B + \overline{A} \cdot C + B \cdot C = A \cdot B + \overline{A} \cdot C \qquad(式4.6) \\ \end{gathered}

证明:原式扩写为A⋅B+A‾⋅C+B⋅C⋅(A+A‾)=A⋅B+A‾⋅C+A⋅B⋅C+A‾⋅B⋅C=A⋅B⋅(A⋅B+C)+A‾⋅C⋅(A‾⋅C+B)=A⋅B+A‾⋅C,得证 \begin{gathered} 证明:原式扩写为A \cdot B + \overline{A} \cdot C + B \cdot C \cdot (A + \overline{A})=A \cdot B + \overline{A} \cdot C + A \cdot B \cdot C + \overline{A} \cdot B \cdot C = A \cdot B \cdot (A \cdot B + C) + \overline{A} \cdot C \cdot (\overline{A} \cdot C + B) = A \cdot B + \overline{A} \cdot C,得证 \\\\\\ \end{gathered}

A⋅B+A‾⋅C+B⋅C⋅D=A⋅B+A‾⋅C(式4.7) \begin{gathered} A \cdot B + \overline{A} \cdot C + B \cdot C \cdot D = A \cdot B + \overline{A} \cdot C \qquad(式4.7) \end{gathered}

证明:与式4.6同理 \begin{gathered} 证明:与式4.6同理 \end{gathered}


计算机组成原理 数字电路 CPU 逻辑门电路

本博客所有文章除特别声明外，均采用 CC BY-SA 3.0协议 。转载请注明出处！